L1和L2正则化的实际案例
在机器学习中,L1和L2正则化是常用的防止过拟合的技术。它们通过在损失函数中添加正则化项来限制模型的复杂度。下面我们将通过实际案例来介绍L1和L2正则化的应用。
1.特征选择
案例描述在许多机器学习任务中,特征选择是一个重要的环节。特别是在文本处理中,特征数量可能会非常大。通过使用L1正则化,我们可以得到一个稀疏的权值矩阵,这意味着只有少数特征对模型有贡献,其余的特征几乎不产生影响。这有助于我们识别出最重要的特征,从而简化模型并提高泛化能力。
案例分析例如,在疾病预测中,我们可能需要考虑成千上万种潜在的风险因素。通过L1正则化的特征选择,我们可以发现只有几个关键因素与疾病的发生率有关。这样,医生在分析患者状况时就可以更加专注于这些关键因素,从而提高诊断的效率和准确性。
2.防止过拟合
案例描述过拟合是机器学习中的一个常见问题,它发生在模型在训练数据上表现很好,但在新数据上表现较差的情况。L1和L2正则化都可以用来防止过拟合。L2正则化通过减小参数值的大小来降低模型的复杂度,而L1正则化则通过产生稀疏权值矩阵来简化模型。
案例分析以银行信用评分系统为例,银行需要预测哪些客户有可能违约。如果模型过于复杂,可能会过度拟合训练数据,导致对新客户的预测效果不佳。通过使用L1或L2正则化,银行可以设置一个合理的复杂度阈值,使得模型既能很好地拟合训练数据,又能保持足够的泛化能力,从而提高整体的信贷评估性能。
3.处理共线性问题
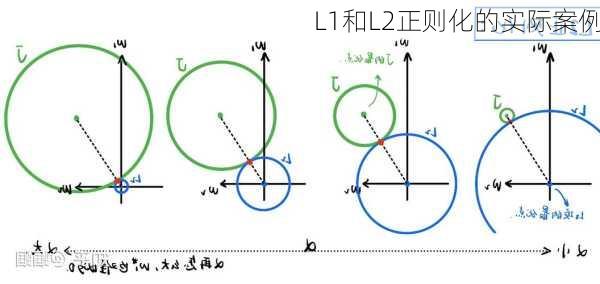 案例描述
案例描述共线性是指模型中的多个特征之间存在高度的相关性。这可能导致权重系数变得不稳定,从而影响模型的性能。L1正则化可以通过将权重系数压缩到较小的范围来缓解共线性问题。
案例分析在一个股票市场预测的例子中,可能会有许多经济指标(如GDP、通货膨胀率等)相互关联。如果直接使用这些指标进行预测,可能会导致模型在权重调整时出现问题。通过引入L1正则化,可以有效地减少特征之间的共线性,从而使模型更加稳健。
以上就是L1和L2正则化的实际案例。在实际应用中,我们需要根据具体的问题和数据特性来选择合适的正则化方法。同时,正则化不仅可以帮助我们构建更有效的模型,还能提供关于哪些特征对目标变量有重要影响的洞见。