在回归问题中,Rsquare(Rsquared)是一个常用的评估指标,它表示模型能够解释的观测数据变异的比例。以下是Rsquare的具体含义:
1.Rsquare的基本定义和计算
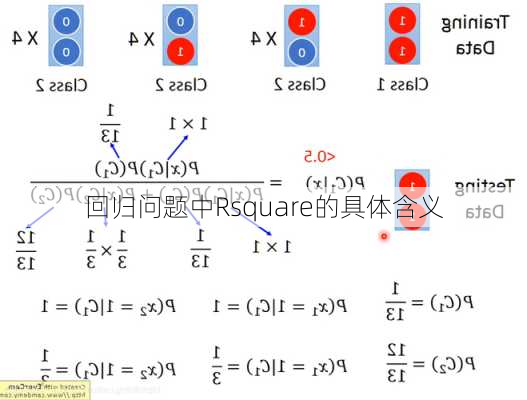
Rsquare,也称为决定系数,是通过比较预测数据与原始数据对应点的误差的平方和(SSE)与总平方和(SST)来计算的。总平方和是观测到的真实值与真实值的均值之间的差的平方和,而误差平方和则是预测值和样本值之间的差异情况。Rsquare的计算公式为:R^2=1SS_res/SST。这个比例越接近1,表示模型对数据的拟合程度越好。
2.Rsquare的物理意义
Rsquare的物理意义是自变量能够解释因变量的变化比例。例如,如果R^2=0.8,表示自变量能够解释80%关于因变量的变化。这说明模型在一定程度上揭示了因变量随自变量变化的趋势。
3.Rsquare的影响因素
在建立回归模型时,增加一个特征变量可能会导致Rsquared增大。这是因为模型有更多的自由度来拟合数据,从而提高了Rsquared的值。然而,这种情况下也需要考虑是否存在多重共线性的问题,即自变量之间存在高度的相关性。此外,如果添加的变量并不具有实际意义,仅仅是为了提高Rsquared,这样的模型可能并没有实际价值。
4.Rsquare与其他评估指标的关系
Rsquare可以反映出模型的总体表现,但它并不能反映模型的预测误差。因此,在模型选择时,除了考虑Rsquare之外,还需要考虑其他评估指标,如均方误差(MSE)、均方根误差(RMSE)和平均绝对误差(MAE)等。这些指标可以提供关于模型预测精度的信息。
5.Rsquare的应用场景
Rsquare广泛应用于各种回归问题中,特别是在评估线性回归模型的拟合程度时。它是一个常见的评估指标,可以帮助我们了解模型对数据变化的解释能力。
总的来说,Rsquare是衡量回归模型性能的重要指标,它反映了模型对观测数据变异性的解释能力。在实际应用中,我们需要结合其他评估指标来综合评价模型的优劣。